ПРИБЛИЖЕННЫЙ АНАЛИЗ БЫСТРОГО БОКОВОГО ДВИЖЕНИЯ

В предыдущем разделе была рассмотрена структура 60і кового возмущенного движения и отмечено, что медленное спираль­ное движение не оказывает существенного влияния на устойчивость самолета/ в то время как характеристики быстрого колебательного движения являются определяющими в оценке его возмущенного дви­жения. Апериодическая составляющая быстрого движения на до — критических углах атаки всегда носит быстро затухающий характер, и поэтому никаких специальных требований к ней не предъявляется.

Чтобы выявить связь быстрого движения и главной его составля­ющей — колебательного движения с аэродинамическими, конструк­тивными характеристиками самолета и режимами полета, проведем
приближенный анализ быстрого бокового Движения, полагая, что возмущения параметров бокового движения и угла атаки самолета невелики. Тогда считая cos а = 1, a sin а = 0, в первом уравнении системы (17.7) кроме слагаемого, содержащего угол крена, можно отбросить слагаемое, содержащее угловую скорость крена. Во вто-

ром уравнении можно пренебречь малой величиной Мух, считая ее равной нулю.

Тогда собственное быстрое движение самолета можно описать системой уравнений следующего вида:

Р = Zpp + соу, <оу ~ Щр Myvcay,
йЛ = Мрр + М%Л + м“%.

В полученной приближенной системе уравнений (17.20), описы­вающей быстрое боковое возмущенное движение, первые два урав­нения описывают движение рыскания, третье уравнение —движе­ние крена.

В силу сделанного допущения о малости угла атаки, движение рыскания можно рассматривать независимо от движения крена.

Если боковое возмущенное движение вызвано начальными воз­мущениями по углу скольжения или угловой скорости рыскания, его можно рассчитать, определив сначала р и со^ из двух первых уравнений, а затем и[34] из третьего уравнения.

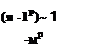Характеристический определитель изолированного движения ры­скания будет иметь вид *

Раскрыв его, получим характеристическое уравнение

Я2 + 2ЛбЯ + со| = 0,

где

2 Лб = -(2В + М»;

(17.23)

Корни уравнения (17.22) получаются комплексными и движение но­сит колебательный характер.

Таким образом, колебательная составляющая бокового возмущен­ного движения при малых углах атаки определяется, главным обра­зом, движением рыскания. Его параметры будут иметь следующий вид:

р = 4e~V sin (їЛо-h-t + ф,) ; (17.24)

иу=Ве ftc<sin (’j/’coe — Лб-f-f ср2).

Подставив эти значения (Ї и и>у в третье уравнение системы (it.20), получим неоднородное дифференциальное уравнение первого по­рядка, описывающее движение крена, вызванное возмущениями в канале рыскания. Характеристическое уравнение этого неоднород­ного уравнения будет иметь вид

= 0. (17.25)

Решение этого уравнения дает большой действительный корень

= (17.26)

Изменение углодой скорости крена в возмущенном движении будет определяться суммой общего решения уравнения (17.25) и частного решения последнего уравнения системы (17.20) с учетом (17.24)

со* = Се4*1* + De~V sin фз). (17.27)

Большой корень определяет, таким образом, быстрое апериодиче­ское движение крена.

Проанализируем подробнее составляющую быстрого бокового движения, определяемую движением рыскания. Если она имеет колебательный характер, то при малых углах атаки эти колебания

—Р (|)

всегда будут затухающими, так как Z <0, Муу < 0. Неустойчи­вость движения может иметь только апериодический характер.

Устойчивость движения рыскания при малых углах атаки будет определяться неравенством со| > 0 при

По аналогии с продольным Движением ор можно назвать сте­пенью статической устойчивости по каналу рыскания. Из формул

(17.28) , (17.29) видно, что, если самолет обладает флюгерной стати­ческой устойчивостью, движение в канале рыскания будет устой­чивым.

Такой вывод справедлив, если в опорном невозмущенном режиме угол атаки мал. При полете на больших углах атаки, которые для современных самолетов могут достигать значений я/6 и более, суще­ственное влияние на движение рыскания оказывает движение крена.

Чтобы проанализировать это влияние, отбросим из первого урав­нения системы (17.7) слагаемые, содержащие углы крена и скольже­ния. Эти слагаемые определяют поперечную силу. Их влияние на быстрое движение невелико, так как они определяют движение цен­тра масс. Зато оставим в уравнении член, содержащий угловую ско­рость крена. Во втором и третьем уравнениях условно отбросим сла­гаемые, определяющие демпфирование.

. Тогда уравнения собственного быстрого движения будут иметь вид _ _

Р № cosa coj, + sinaco*; <й*«./И*р. (17.30)

Дифференцируя первое уравнение по времени и подставляя в него значение производных от угловых скоростей из двух последних уравнений системы (17.30), получим

_ Р — (cos аМу + sin аМ?) р = 0. (17.31)

Соответствующее характеристическое уравнение имеет вид

К2 — ^cosam^ + sinam£y^^==0. (17.32)

Оно не будет иметь положительных корней при условии

— |cos amj) |-sin am*-у^ > 0. (17.33)

Это условие устойчивости движения рыскания.

Из неравенства (17.33) следует, что наличие флюгерной устойчи­вости еще не гарантирует устойчивости движения рыскания и, наобо­рот, при отсутствии флюгерной статической устойчивости Движение рыскания может быть устойчиво благодаря влиянию канала крена. Влияние этого канала тем больше, чем больше углы атаки. На самом деле взаимодействие движений крена и рыскания будет сложнее из-за влияния демпфирующих и спиральных моментов. Границы устойчивости колебательного движения, полученные с учетом этого взаимодействия, приведены на рис. 17.1.